A napfogyatkozásról sok, könnyen megfogalmazható információ jutott el a nagyközönséghez. Ismeretes, hogy a Hold árnyéka egy sáv mentén haladt a Földön, nagyjából nyugatról keletre, változó sebességgel. Az árnyék pár óra alatt futott végig a sávon. A haladási sebesség igen nagy volt a kezdõ és a végsõ helyen.

Ezek a sajátságok, és persze a napfogyatkozás más részletei is pontos csillagászati számításokkal leírhatók. Ám a felsorolt sajátságokról egy egyszerû, közelítõ modell is számot ad - felsõfokú matematikai ismeretek igénybevétele nélkül.

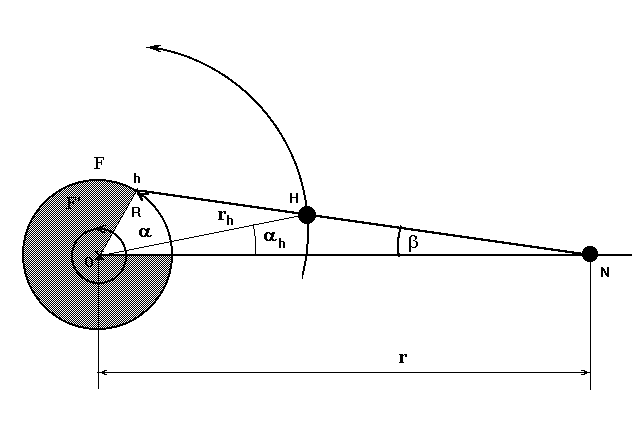
Tekintsük az ábrán látható elrendezést. Legyen F egy O középpontú, R sugarú kör, F’ pedig egy, az F-fel egybeesõ, de állandó w szögsebességgel forgó kör. Legyen H egy olyan pont, amely F körül r_H sugarú körön mozog, w _H állandó szögsebességgel. Az origótól r távolságban pontszerû N fényforrás található. Határozzuk meg H árnyékának, h-nak a mozgását az F’ körvonalon!

Legyen az x tengely az ON egyenes, az ehhez viszonyított szögekkel dolgozunk. Jelöljük a H-hoz tartozó szöget a _H-val, a H árnyékához, h-hoz tartozó szöget a -val. A h, H és N pontok Descartes-koordinátái rendre: h (x = R cosa , y = R sina ), H (x_H = r_H cosa _H, y_H = r_H sina _H ), N (x_N = r, y_N =0). Az ábrából nyilvánvaló, hogy
 
 

Ebbõl az egyenletbõl az a _H szög ismeretében kiszámíthatjuk az a szög értékét. Sokkal egyszerûbb a megoldás, ha feltételezzük, hogy r igen nagy, r >> (x, x_H). Ebben az esetben (1)-bõl az
 
 

közelítõ egyenletet kapjuk. Innen
 
 

Tegyük fel még, hogy t=0 idõben az árnyék éppen az x tengelyen van, azaz
 
 

Az w szögsebességgel forgó F’ körön a h árnyékpont a ’ szögét úgy kapjuk, hogy a -ból levonjuk az F’-nek a forgás miatt t idõ alatt bekövetkezõ w t szögelfordulását:
 
 

Ezzel az árnyékpont mozgását meghatároztuk a forgó F’ körön. Ezek után könnyen megválaszolhatjuk az alábbi kérdéseket.
 

Az árnyék sebessége a t=0 idõpontban.

azaz az árnyék szögsebessége a forgó F’körön
 
 

és így az árnyékpont sebessége t=0-nál:
 
 

Az árnyék teljes tartózkodási ideje az F körön.

Az árnyék –az r>>r_H feltétel miatt - közelítõleg a (0,-R) pontban éri el F-et, és a (0,R) pontban válik le róla. A fogyatkozás alatt H szöge az -a _Hkr értékrõl a _Hkr értékre nõ, ahol

Az árnyék által megtett út

Az árnyék az F körön majdnem egy félkört tesz meg. A forgó F’-n megtett út ennél kisebb: le kell vonnunk azt az utat, amit a forgó F’ egy pontja a t idõtartam alatt megtesz. Tehát a forgó F’-n az árnyék
 

Az árnyék sebessége a végpontoknál

Az ábrából látszik, hogy ugyanahhoz a D a _H szögelforduláshoz más-más ív tartozhat F-en, ezért az árnyék változó sebességgel mozog. A sebesség végtelenhez tart a kezdõ- és végpontnál (a -a Hkr illetve a Hkr szögeknél), mert akkor a fénysugár érinti F-et. A sebesség értékét differenciálással lehetne meghatározni.
 
 
 

Numerikus értékek

Helyettesítsük be a következõ numerikus értékeket:
 
 

R=6400 km

r_H = 60 R = 380000 km

r = 400 r_H = 150 millió km

w = 2 p /T T = 1 nap = 24 óra

w _H = 2 p /T_H T_H = 30 nap
 

Rw = 40000 km/24 óra = 1700 km/óra

r_H w _H = 2 R w ,
 

azaz a Hold keringési sebessége közelítõleg kétszerese a Föld egyenlítõjén a forgásból származó sebességnek. Ezért az árnyékpont sebessége a fenti modellben a napfogyatkozás centrumában, azaz a t=0 idõpontban közel egyenlõ a forgásból eredõ sebességgel, de azzal ellentétes, ez magyarázza a nyugatról keletre való haladást.

A fogyatkozás teljes tartama (7)-bõl közelítõleg

t =1/w = T/2p = 3.8 óra
 

A forgó F’ körön ez alatt az idõ alatt 13500 km-t tesz meg az árnyék.
 
 

Összehasonlítás az 1999. Aug. 11-i napfogyatkozás adataival..

A napfogyatkozás 9:31-kor kezdõdött az Atlanti óceán északi részén, és 12:36-kor a Bengáli Öbölben fejezõdött be, tehát teljes tartama kicsivel több, mint 3 óra. Ez alatt a Hold árnyéka 14 ezer km utat tett meg a Földön.

A napfogyatkozás centruma Románia középsõ részén volt, 11:03-kor. Itt az árnyék sebessége 2400 km/óra volt.
 
 
 

Megjegyzések.

A modell legnagyobb hibája a Föld forgási sebességének számításánál van. A napfogyatkozás centrumának helyén ugyanis a forgásból eredõ sebesség az egyenlítõi értéktõl kisebb. A másik lényeges eltérés abból adódik, hogy a modellel ellentétben a Föld pályasíkja nem merõleges a Föld forgástengelyére. Továbbá, a Hold pályasíkja mintegy 5^o-kal eltér a Földpálya síkjától.

A Föld keringésének elhanyagolása viszont annak ellenére sem jelent hibát, hogy e keringés sebessége jóval nagyobb, mint a forgásból származó sebesség, mivel a Föld és a Hold együtt mozog a Nap körül.

H-t és N-et pontszerûnek tételeztük fel. A teljes fogyatkozás idõtartama a Föld egy pontján természetesen ekkor zérusnak adódik. A pontszerû N pedig csak teljes fogyatkozást okozna, a jelenséget kísérõ részleges fogyatkozáshoz már számolni kellene N méretével is.

Az a határeset, hogy r tart a végtelenhez, annak felel meg, hogy az árnyékot az x tengellyel párhuzamos sugárnyaláb hozza létre.