Galilei-transzformáció és a Galilei-féle relativitás. Összehasonlítás az Einstein-féle relativitási elvvel.

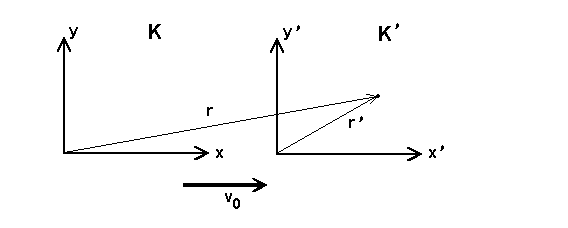
Vegyünk két Descartes-féle koordinátarendszert. K és K’ tengelyei t = 0-kor egybeesnek, K’ az x tengely irányába mozog állandó v₀ sebességgel. Ha egy tömegpont helyét az x, y, z koordináták adják meg a K rendszerben, x’, y’, z’ pedig a K’ rendszerben, akkor

x’ = x - v₀t

y’ = y

z’ = z

t’ = t

A K koordinátarendszer meghatároz egy R vonatkoztatási rendszert, a K’ pedig egy R’ vonatkoztatási rendszert. A két vonatkoztatási rendszer egymáshoz képest v₀ állandó sebességű egyenesvonalú egyenletes transzlációt végez. R-ben a tömegpont sebessége v, R’-ben v’ = v-v₀. Ez a sebességösszeadás klasszikus formulája, ami közvetlen következménye a Galilei-transzformációnak. A tömegpont gyorsulása a két rendszerben egyenlő: a’ = a, mert v₀ állandó. Ezért a mozgásegyenlet invariáns a Galilei-transzformációra, azaz

ma = F = ma’

Mivel minden mechanikai probléma visszavezethető a tömegpont mozgásegyenletére, ezzel bebizonyítottuk a Galilei-féle relativitási elvet: mechanikai szempontból az egymáshoz képest egyenesvonalú egyenletes transzlációt végző vonatkoztatási rendszerek egyenértékűek. Ha R inerciarendszer, akkor R’ is inerciarendszer.

Ha ma (jelző nélkül) relativitáselvről beszélünk, akkor az Einstein-féle relativitáselvet értjük alatta. Ez annyiban általánosabb, mint a Galilei-féle, hogy a két rendszer egyenértékűségét nemcsak a mechanika szempontjából, hanem általában, minden fizikai szempontból mondja ki. Az Einstein-féle relativitáselméletben a Galilei- transzformáció helyébe a Lorentz-transzformáció lép. Ellentétben a Galilei-transzformációval, itt az idő a két rendszerben nem azonos, nincs egységes világidő, hanem minden inerciarendszerhez külön rendszeridő tartozik. Az Einstein-féle relativitáselméletnek számos olyan következménye van, ami a klasszikus szemléletünkkel ellentétes (az egyidejűség relatív, mozgó rendszerben a távolságok lerövidülnek, az időtartamok meghosszabbodnak, a sebességösszeadás klasszikus képlete nem alkalmazható, stb.).

Egy tömegpont helyét görbevonalú koordinátarendszerben három koordináta adja meg. Általában egy f szabadsági fokú mechanikai rendszer helyét, helyzetét f általánosított koordinátával adhatjuk meg: q = (q₁,…,q_f).

Tekintsünk egy f szabadsági fokú konzervatív mechanikai rendszert, amelynek potenciális energiája E_pot, kinetikus energiája E_kin. Az előbbi az általános koordináták függvénye, az utóbbiról tételezzük fel, hogy a általánosított sebességektől négyzetesen függ.

Definiáljuk a q_i koordinátához rendelt általánosított impulzust, p_i-t a következőképpen:

A rendszer Hamilton-függvényét megkapjuk, ha a mechanikai energiát kifejezzük mint az általános koordináták és impulzusok függvényét:

H(q,p) = E_kin + E_pot.

A Hamilton-függvény segítségével megadhatók a

A Hamilton-egyenletek megoldása nélkül is könnyen látható, hogy H értéke a mozgás közben állandó

H(q,p) = E₀ (konstans: a mechanikai energia kezdeti értéke)

A mechanikai energia megmaradási tétele következtében tehát a fázistérben minden trajektória rajta van egy állandó energiájú szintfelületen, az energia értékét a kezdeti feltételek határozzák meg.

Kiindulunk a harmonikus oszcillátornak a newtoni mechanikából már ismert formuláiból, és eljutunk a Hamilton-függvényhez és a harmonikus oszcillátor hamiltoni tárgyalásához.

A harmonikus oszcillátor szabadsági foka 1, legyen a koordináta q = x, a sebesség így: . A kinetikus és a potenciális energia a newtoni mechanikából ismert:

Hogy innen a Hamilton formalizmushoz eljussunk, be kell vezetnünk a kanonikus impulzust:

(Látható, hogy ez most éppen a közönséges impulzus.)

A fentiek alapján a Hamilton-függvény:

,

a Hamilton-egyenletek pedig:

(Az utóbbi egyenlet éppen az impulzustétel.)

A Hamilton-egyenletek önmagukban a harmonikus oszcillátor teljes leírását adják, korábbi ismeretek nem szükségesek.

A H = E₀ (konst) összefüggés (a mechanikai energia megmaradása) most (f = 1 esetén) közvetlenül a trajektóriák egyenletét adja meg a fázistérben:

A trajektóriák tehát origó középpontú ellipszisek:

Az időfüggést a Hamilton-egyenletek megoldása adja. A mozgás időben periodikus, a harmonikus rezgés periódusideje

,

tehát csak a rendszer adataitól függ; minden trajektóriára azonos.

Tekintsünk most egy merev testet, ami rögzített tengely körül foroghat. A szabadsági fok 1. Koordinátának most a szöget célszerű választani, az általános sebesség pedig a szögsebesség:

A kinetikus energia:

, q a tehetetlenségi nyomaték.

Az általános impulzus:

,

azaz az általános impulzus most éppen az impulzusmomentum.

Ha külső erő nem hat (szabad rotátor), akkor E_pot = 0.

A szabad rotátor Hamilton-függvénye:

H = p²/2q

A Hamilton-egyenletek:

Tehát p állandó (perdületmegmaradás). Ebből jön, hogy a szabad rotátor egyenletes forgómozgást végez állandó, szögsebességgel.

Jegyzetkiegészítés

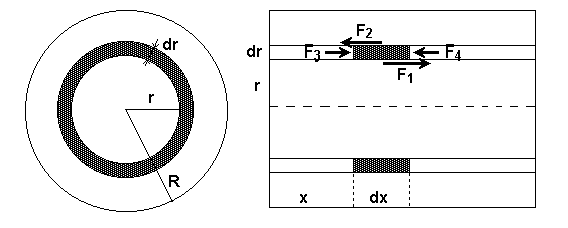
Feltételezzük, hogy az áramlás hengerszimmetrikus. Legyen x a cső tengelye, az erre merőleges y, z síkban pedig vezessük be az r, a polárkoordinátákat. Vegyünk egy hengergyűrűt r és r+dr sugarak illetve x és x+dx között. A nyomás x-től függ, a tengely mentén az áramlás irányában csökken, de sugárirányban nem változik, ez kimutatható. A hengergyűrű palástjaira ható nyomóerők eredője zérus (a hengerszimmetria miatt). A belső és külső paláston nyíróerők hatnak (a sebesség sugárirányban történő változása miatt), a belső paláston előre (F₁), a külső paláston vissza (F₂), ezek eredője egy előre mutató erő. A hengergyűrű alaplapján és fedőlapján a nyomóerők (F₃, F₄) egy visszafelé mutató eredőt adnak. Ez tart egyensúlyt stacionárius áramlásnál a nyíróerők eredőjével.

F₃ = p(x) × 2rp dr

A kapott differenciálegyenlet szeparálható, a megoldás:

tehát a sebességprofil parabolikus, legnagyobb a sebesség a cső közepén, falánál zérus.